- on Desarguesian Affine and Projective Planes
-
Given a quadrangle G(1:1:1)Ga(-1:1:1)Gb(1:-1:1)Gc(1:1:-1) together with its diapleural triangle A(1:0:0)B(0:1:0)C(0:0:1) and its diagonals GA(0:1:-1)GBC(0:1:1),GB(-1:0:1)GCA(1:0:1),GC(1:-1:0)GAB(1:1:0), then B(0:1:0),C(0:0:1) and GA(0:1:-1),GBC(0:1:1) are mutually harmonic conjugates. So are C(0:0:1),A(1:0:0) and GB(-1:0:1)GCA(1:0:1) and A(1:0:0),B(0:1:0) and GC(1:-1:0)GAB(1:1:0). Due to the principle of duality, the above propositions hold for a quadrilateral g(x+y+z=0)ga(-x+y+z=0)gb(x-y+z=0)gc(x+y-z=0) together with its diagonal trilateral a(x=0)b(y=0)c(z=0) and its diagonals gA(y-z=0)gBC(y+z=0),gB(z-x=0)gCA(z+x=0),gC(x-y=0)gAB(x+y=0). Given two points A,B on a projective(or affine) planes over a division ring with characteristic not 2 with its homogenous coordinates, then A,B and C=A+B,D=A-B are mutually harmonic conjugates because of A=C+D,B=C-D.
- on the Extended Complex Plane
-
Given a pair of points A,B and a point P on the extended complex plane, the Möbius transformation P↦P'=(A(P-B)+B(P-A))/((P-B)+(P-A)) is an involution, which is called the harmonic conjugation with fixed points A and B. We say that P,P' and A.B are the mutual harmonic conjugates. In other words, A and B are the image pair of the harmonic conjugation with fixed points P and P'. Given a triangle on the extended complex plane, we can get the cosymmedian triangles ABC and A'B'C' as the following table:
Harmonic Conjugate Pairs AA' and BB' and CC' on the Extended Complex Plane Harmonic Conjugates Formulas AA' BC
AA' B'C'A'=(B(A-C)+C(A-B))/((A-C)+(A-B))=(B'(A-C')+C'(A-B'))/((A-C')+(A-B'))
A=(B(A'-C)+C(A'-B))/((A'-C)+(A'-B))=(B'(A'-C')+C'(A'-B'))/((A'-C')+(A'-B'))BB' CA
BB' C'A'B'=(C(B-A)+A(B-C))/((B-A)+(B-C))=(C'(B-A')+A'(B-C'))/((B-A')+(B-C'))
B=(C(B'-A)+A(B'-C))/((B'-A)+(B'-C))=(C'(B'-A')+A'(B'-C'))/((B'-A')+(B'-C'))CC' AB
CC' A'B'C'=(A(C-B)+B(C-A))/((C-B)+(C-A))=(A'(C-B')+B'(C-A'))/((C-B')+(C-A'))
C=(A(C'-B)+B(C'-A))/((C'-B)+(C'-A))=(A'(C'-B')+B'(C'-A'))/((C'-B')+(C'-A'))CA BB' AB CC'
C'A' BB' A'B' CC'A=(B(C-B')+B'(C-B))/((C-B')+(C-B))=(C(B-C')+C'(B-C))/((B-C')+(B-C))
A'=(B(C'-B')+B'(C'-B))/((C'-B')+(C'-B))=(C(B'-C')+C'(B'-C))/((B'-C')+(B'-C))AB CC' BC AA'
A'B' CC' B'C' AA'B=(C(A-C')+C'(A-C))/((A-C')+(A-C))=(A(C-A')+A'(C-A))/((C-A')+(C-A))
B'=(C(A'-C')+C'(A'-C))/((A'-C')+(A'-C))=(A(C'-A')+A'(C'-A))/((C'-A')+(C'-A))BC AA' CA BB'
B'C' AA' C'A' BB'C=(A(B-A')+A'(B-A))/((B-A')+(B-A))=(B(A-B')+B'(A-B))/((A-B')+(A-B))
C'=(A(B'-A')+A'(B'-A))/((B'-A')+(B'-A))=(B(A'-B')+B'(A'-B))/((A'-B')+(A'-B))
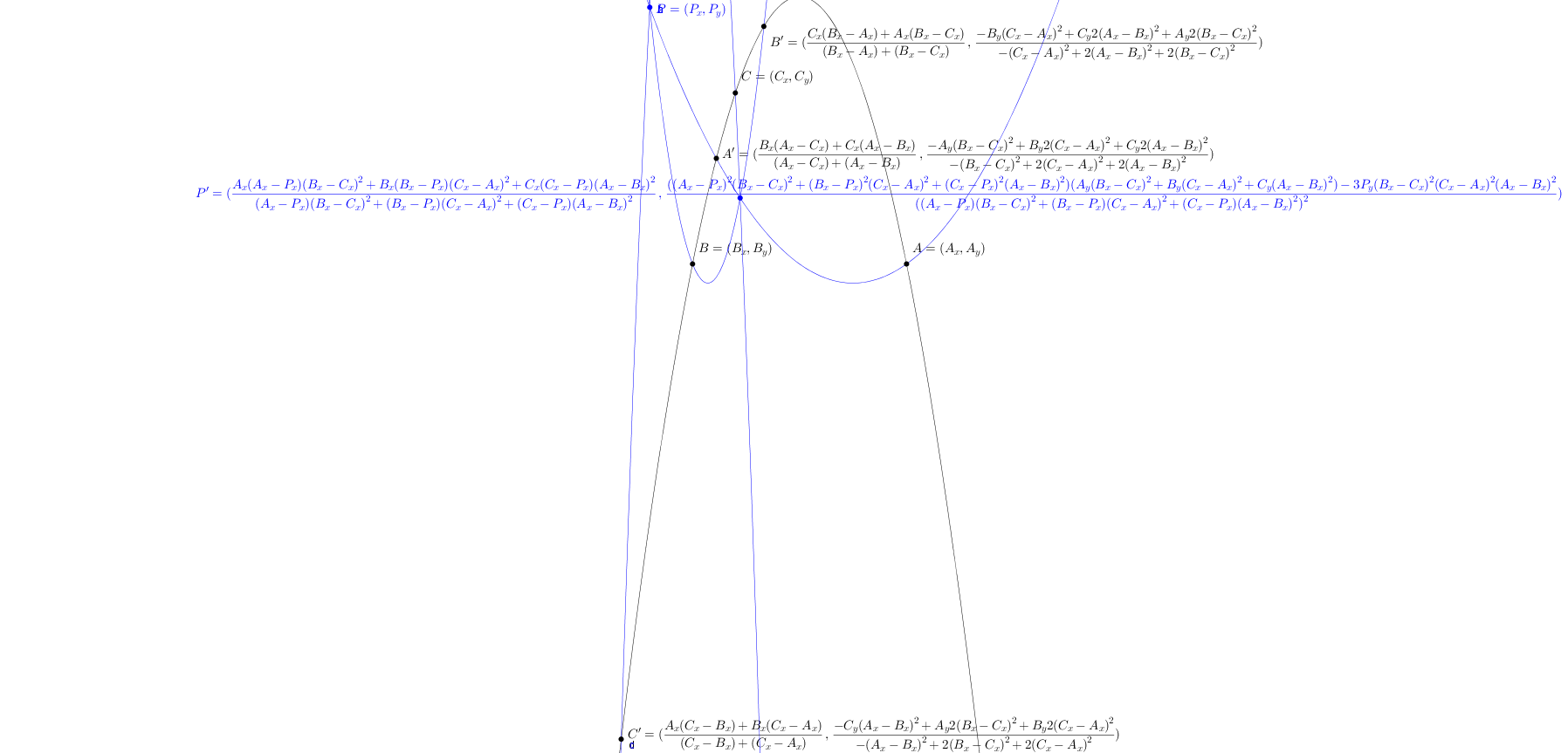
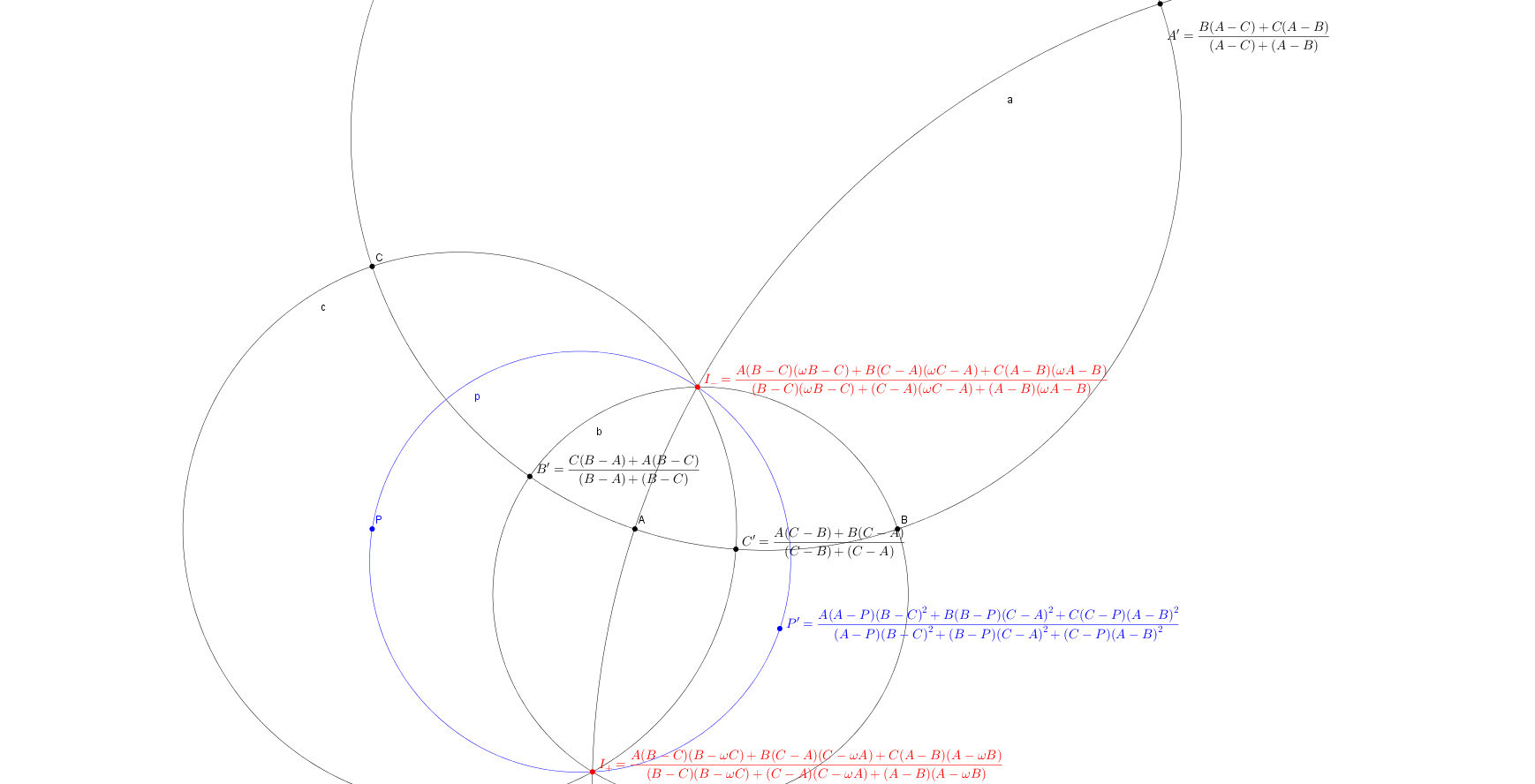
Given a triangle ABC and a point P on the extended complex plane, the harmonic conjugatation with the isodynamic points I+=(A(B-C)(B-ωC)+B(C-A)(C-ωA)+C(A-B)(A-ωB))/((B-C)(B-ωC)+(C-A)(C-ωA)+(A-B)(A-ωB)) and I-=(A(B-C)(ωB-C)+B(C-A)(ωC-A)+C(A-B)(ωA-B))/((B-C)(ωB-C)+(C-A)(ωC-A)+(A-B)(ωA-B))(where ω is the imaginary cube root of 1) of ABC as the fixed points is the isodynamic harmonic conjugation P↦P'=(A(A-P)(B-C)2+B(B-P)(C-A)2+C(C-P)(A-B)2)/((A-P)(B-C)2+(B-P)(C-A)2+(C-P)(A-B)2). The cosymmedian triangles ABC and A'B'C' are images of the isodynamic harmonic conjugation. If P is the point at infinity, P' is the Schoute center X(187) of ABC. P.S. In fact, this conjugation is an involution of every commutative field.